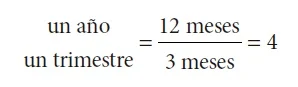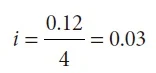Qúe es el diagrama de flujo de caja y cómo se utiliza

Concepto y definición:

Dado que todas las operaciones intervienen dos clases de valores a lo largo del tiempo, los ingresos y los egresos relacionados con la operación, se llama flujo de caja a la secuencia que representa esos valores, o, lo que es lo mismo, a la secuencia de entradas y salidas de capitales durante el tiempo de la operación financiera. Con el fin de visualizar esta operación, suelen representarse tales valores sobre un segmento de recta que tenga como longitud el tiempo que dure la operación medido en periodos. Esta representación gráfica es conocida con los nombres de diagrama de flujo de caja o diagrama de tiempo valor. También se ha convenido en que los valores se señalen con una flecha, hacia arriba sin son ingresos y hacia abajo sin son egresos; sin embargo, este orden puede invertirse debido a que no afecta los resultados.

El diagrama de flujo de efectivo es una excelente herramienta que nos ayuda a visualizar cómo fluye el dinero a través del tiempo. En esta herramienta el tiempo se representa como una linea recta horizontal, que fluye de izquierda (inicio)  a derecha (final). el dinero se representa con flechas hacia arriba y hacia abajo, una flecha hacia arriba siempre va a representar ganancias, beneficios e ingresos; mientras que la flecha hacia abajo siempre va a representar inversión, desembolso, perdida, costo, etc.

Es importante destacar que en una transacción financiera siempre hay dos partes, un comprador y un vendedor, un prestador y un prestatario y que los diagramas de flujo de efectivo de ambos son como imágenes de espejo.

¿Cómo se utilizar el Diagrama de flujo de caja?

Vamos a explicar lo antes mencionado con algunos ejemplos:

Ejemplo 1:

El señor Pedro hace una inversión (egreso) hoy por un valor de $10,000 y recibe unos ingresos de $4,000 dentro de cuatro meses y de $8,000 dentro de diez meses, con estos acontecimientos podemos realizar el diagrama de flujo de caja para el señor Pedro.

Un banco cercano a la vivienda del señor Pedro le otorga un préstamo por un valor de $ 5,000,000 y le exige que la deuda sea cubierta en tres pagos, así $2,000,000 dentro de seis meses, $2,500,000 dentro de 8 meses y $2,300,000 dentro de un año. Se pide representar los flujos de caja desde el punto de vista del banco y del señor Pedro.

La siguiente imagen representa el diagrama de flujo de caja del Banco, esta entidad es la parte acreedora, inicialmente desembolsa (egreso)  $5,000,000 y recibe del señor pedro (ingresos) $2,000,000 dentro de 6 meses, $2,500,000 dentro de 10 meses y $ 2,300,000 dentro de 12 meses.

El tiempo cero es el momento en que se realiza la primera transacción cuando el banco desembolsa y el seño pedro recibe el dinero.

Igualmente, desde el punto de vista del señor Pedro se puede dibujar el diagrama de flujo de caja, recibiendo el señor Pedro la cantidad de $5,000,000 (Ingresos)  y pagando (egresos) pagando $2,000,000, $2,500,000, $2,300,000 en 6, 10 y 12 meses respectivamente.

Fuente:

Matemática financiera 5ta. edición (Jaime A. García)

Fundamentos de Ingeniería Económica (Gabriel Vaca Urbina)

Caracteristicas de las inversiones

Podemos afirmar que las inversiones son la aplicación de recursos con el objetivo de obtener un beneficio futuro, las inversiones no es una actividad aplicada solo para empresas o organizaciones ya constituidas, el ejercicio de invertir lo puede realizar cualquier persona que desee obtener un resultado económico, el tema de las inversiones es de interés para cualquier persona independientemente de su profesión o si es emprendedor o no, en esta publicación comenzamos con el estudio de los proyectos de inversión, a continuación les dejo las características de las inversiones.

Sin duda los motivos principales por las que empresas y personas naturales invierten su dinero es porque tienen excedentes de recursos y también por necesidad, estos elementos los estudiaremos más adelante

Características de las inversiones:

Beneficios:

Cuando se aplican recursos a alguna actividad se realiza una inversión. Siempre existe la expectativa de obtener un resultado, producto o beneficio mayor que si no se realizara la inversión. El beneficio es el elemento que nos impulsa a invertir, el beneficio final depende de muchos factores  en el que podemos destacar: los riesgos, la habilidad y el conocimiento del negocio y la correcta implementación de las estrategias fijadas en el plan de inversión.

Tiempo:

Toda aplicación de recursos se hace con la confianza de recuperar la inversión en el menor tiempo posible. La característica principal de las inversiones de capital es que su recuperación es a largo plazo, ya que por lo general se localizan en activos cuya recuperación es a un plazo mayor de un año; tal es el caso de la compra de maquinaria, equipo de transporte, la fundación de una nueva empresa, la fabricación de una nueva línea de productos y/o servicios, por citar sólo algunos ejemplos.

Riesgo:

Es la probabilidad de perder la inversión por diversos motivos asociados con la volatilidad de las variables que contribuyen a generar los rendimientos de la inversión; por ejemplo, tasas de interés de las deudas, tasas de interés en los créditos bancarios que influyen directamente en el consumo de la población, etc. Cabe destacar que, cuando una empresa otorga crédito a sus clientes para que adquieran sus productos con la intervención de un banco, el costo de financiamiento para los consumidores se incrementa, situación que desalienta a los consumidores y modifica el nivel de ventas de la empresa, con lo cual disminuyen las utilidades. 

En el caso de un incremento de la inflación en el país donde se radicó la inversión, se genera un aumento de los precios de los insumos necesarios para producir los bienes y servicios, lo cual reduce el margen de utilidad y, por consiguiente, aumenta el plazo de recuperación de la inversión y disminuye la tasa de recuperación de ésta. Otra variable que influye en la magnitud de los rendimientos es el tipo de cambio.

Una depreciación del tipo de cambio encarece el costo en moneda nacional de las materias primas e insumos importados, a la vez que se eleva los costos financieros de las empresas que mantienen pasivos en moneda extranjera. Por lo tanto, una depreciación del tipo de cambio provoca el fenómeno conocido como inflación de costos o estanflación, situación en la cual la trayectoria ascendente de los precios coincide con el desplome de la producción.

Todos estos factores que incluyen a los ingresos, los costos y la incertidumbre se denominan riesgos de la inversión, pues pueden repercutir de manera negativa en la recuperación de la inversión.

Medio ambiente de las inversiones:

Las empresas o cualquier tipo de inversión funcionan en ambientes altamente competitivos debido a la existencia de otras empresas que persiguen los mismos objetivos; además, todas las entidades se encuentran expuestas a los vaivenes de las variables económicas, dependen del país en que se desarrollen y de su vulnerabilidad a la economía global. Por ejemplo, si la inversión se realiza en una empresa cuyo objetivo es la fabricación de un producto o la prestación de un servicio y existe una gran cantidad de compañías que, con el mismo producto o servicio han capturado gran parte del mercado actual y que cuentan con un departamento de investigación y desarrollo que les ayuda a detectar los cambios de gustos de los consumidores, la tecnología aplicable en los procesos de elaboración y materiales de los productos o servicios generados, tendencias de los mercados, productos sustitutos etc., el ambiente se caracterizará por una competencia dinámica, que hace más difícil el logro de los objetivos previamente planteados. Si la tecnología es accesible a los productores y permite el desarrollo de mejores productos existen mayores posibilidades de competir con otras empresas. En ese sentido, el acceso a la tecnología es un factor fundamental en el análisis del ambiente de las inversiones. Por otra parte, el nivel de ingresos de la población determina su poder adquisitivo; si ésta goza de un mayor nivel de ingresos tendrá más poder de compra, y viceversa. Esta característica de la población afecta de manera directa el volumen de ventas de las empresas o proyectos de inversión y, por consiguiente, repercute en el nivel de utilidades, el cual es fundamental para recuperar la inversión. La lista de factores que condicionan el medio ambiente pero que también limitan o facilitan el funcionamiento de las empresas y/o proyectos de inversión es extensa.

Sin duda los motivos principales por las que empresas y personas naturales invierten su dinero es porque tienen excedentes de recursos y también por necesidad, estos elementos los estudiaremos más adelante.

Fuente de apoyo:

Proyectos de inversión, evaluación y formulación 

José Antonio Morales Castro 

Arturo Morales Castro 

Matemática financiera: interés compuesto definición y ejemplo

El dinero y el tiempo son dos factores que se encuentran estrechamente ligados con la vida de las y personas y de los negocios. Cuando se generan excedentes de efectivo, se ahorran durante un periodo determinado a fi n de ganar un interés que aumente el capital original disponible; en otras ocasiones, en cambio, se tiene necesidad de recursos financieros durante un tiempo y se debe pagar un interés por su uso.

En periodos cortos por lo general se utiliza, como ya se vio, el interés simple. En periodos

largos, sin embargo, se utilizará casi exclusivamente el interés compuesto.

También te puede interesar:

Valor del dinero en el tiempo

Matemática financiera: Operaciones con descuento

Generalidades del interés simple

Interés simple e interés compuesto, diferencia:

A continuación para una mejor comprensión del tema, les dejo algunas definiciones de interés compuesto que he encontrado en algunos libros que consulte para desarrollar el tema, el nombre de los autores y de los libros los dejo al final.

Definición:

La definición del interés compuesto es esencial para entender las matemáticas financieras:

1) En el interés simple el capital que genera el interés permanece constante todo el tiempo que dura el préstamo. En cambio, en el interés compuesto el interés generado en un periodo dado se convierte en capital para el siguiente periodo. 

2) El interés se puede definir como la operación financiera en la que el capital aumenta al final de cada periodo por adición de los intereses vencidos.

3) En el interés simple el capital original sobre el que se calculan los intereses permanece sin variación alguna durante todo el tiempo que dura la operación. En el interés compuesto, en cambio, los intereses que se generan se suman al capital original en periodos establecidos y, a su vez, van a generar un nuevo interés adicional en el siguiente lapso.

En este caso se dice que el interés se capitaliza y que se está en presencia de una operación de interés compuesto.

En estas operaciones, el capital no es constante a través del tiempo, pues aumenta al final de cada periodo por la adición de los interés ganados de acuerdo con la tasa convenida.

Esta diferencia puede captarse con claridad por medio del ejemplo siguiente:

Ejemplo 1:

Suponga que se depositan $100 000 en una cuenta de ahorros que paga 10% de interés semestral (20% de interés anual). ¿Cuál será el interés ganado al cabo de 6 meses?

I = Cit

I = 100 000(0.10)(1)

I = 10 000

Suponga que se depositan otros $100 000 en una cuenta de valores que paga 20% de interés convertible trimestralmente. ¿Cuál será el interés ganado al cabo de 6 meses?

(Nota: La tasa de interés nominal es la misma en ambos casos: 5% trimestral = 20%

anual.)

i trimestral

20% anual / 4 trimestres = 5%

1er. trimestre I = Cit

I = 100 000(0.05)(1)

I = 5 000

2do. trimestre I = (C + I)it

I = (100 000 + 5 000)(0.05)(1)

I = 105 000 (0.05)(1)

I = 5 250

I total = I 1er. trimestre + I 2do. trimestre

I total = 5 000 + 5 250

I = 10 250

En este caso, el interés es superior al que se ganó en el anterior, pues al fi nal del 1er. trimestre al capital original se le suma el interés ganado, con lo cual el total del segundo trimestre será superior al del primero.

Por lo tanto, el capital se incrementa por la adición de los intereses al final de cada periodo y éstos, a su vez, se incrementan pues son calculados sobre una base cada vez mayor. La cantidad acumulada al final de la operación se conoce como monto compuesto.

La diferencia entre el monto compuesto y el capital original es el interés compuesto. 

Periodo de capitalización

El interés puede ser convertido en capital anual, semestral, trimestral y mensual, etc. A dicho periodo se le da el nombre de “periodo de capitalización”. Al número de veces que el interés se capitaliza durante un año se le denomina frecuencia de conversión.

¿Cuál es la frecuencia de conversión de un depósito bancario que paga 5% de interés capitalizable

trimestralmente?

La frecuencia de conversión es igual a 4. El periodo de capitalización es trimestral. 

Tasa de interés compuesto

Por lo general, la tasa de interés se expresa en forma anual. Además, junto con ella se indica, si es necesario, su periodo de capitalización.

28% anual capitalizable mensualmente

10% anual capitalizable semestralmente

6% anual capitalizable trimestralmente

Si el interés se expresa sin mención alguna respecto de su capitalización, se entiende que ésta es anual.

Es muy importante que, para la solución de cualquier problema de interés compuesto, el interés anual sea convertido a la tasa que corresponda de acuerdo con el periodo de capitalización que se establezca; si el interés se capitaliza mensualmente el interés anual debe transformarse en interés mensual; si es trimestralmente, a interés trimestral, etcétera.

El periodo de capitalización y la tasa de interés compuesto siempre deben ser equivalentes. Así, en el ejemplo inicial, el interés de 20% anual fue transformado en interés trimestral de 5% para hacerlo equivalente al periodo de capitalización que allí se mencionaba.

En este momento pueden establecerse dos conclusiones :

a) El interés compuesto es mayor que el interés simple. Esto se debe a que el primero gana intereses por sí mismo, en tanto que el segundo no.

b) A mayor frecuencia de conversión, mayor será el interés que se obtenga si la tasa anual nominal es igual; así, un depósito bancario que obtenga intereses en forma mensual tendrá mayor rendimiento que uno que los capitalice trimestralmente y éste, a su vez, será mayor que otro que los logre cada semestre.

En forma más clara se observa el comportamiento del interés simple y el interés compuesto en una gráfica. Considere el siguiente ejemplo:

El monto a interés simple crece en forma aritmética y su gráfica es una línea recta. Sus incrementos son constantes y el interés del quinto año es igual al del primero. Su ecuación es la de una línea recta cuya pendiente o razón de incremento está dada por la tasa de interés.

En cambio, una cantidad que se coloca a interés compuesto crece en forma geométrica y su gráfica corresponde a la de una función exponencial:

Sus incrementos son variables. Como se puede apreciar en la gráfica, cada periodo presenta un incremento mayor al del periodo anterior. Su ecuación es la de una línea curva que asciende a velocidad cada vez mayor.

Monto compuesto:

El monto compuesto, como ya se ha explicado, es el resultado que se obtiene al sumar al capital original el interés compuesto. Si se dispone de un capital C y se invierte en un banco y se desea conocer el monto M del cual se dispondrá al final del periodo, sólo debe agregársele el interés I ganado.

M = C + I 

pero I = Cit

cuando t = 1, I = Ci

por lo que M = C + Ci que factorizando da

M = C(1 + i)

Como puede verse, el monto de un capital al final de un periodo se obtiene multiplicándolo

por el factor (1 + i). De esta manera, al final del segundo periodo se tiene que:

Al final del tercer periodo se tiene que:

y así sucesivamente. Esta sucesión de montos forma una progresión geométrica cuyo n-ésimo término es igual a:

Esta ecuación se conoce como fórmula del monto a interés compuesto.

Ejemplo 2:

Se depositan $50 000 en un banco a una tasa de interés de 18% anual capitalizable mensualmente.

¿Cuál será el monto acumulado en 2 años?

Solución:

Como se estableció previamente, el monto a interés compuesto se calcula mediante la ecuación

Se destaca nuevamente que la definición de periodo debe ser la misma para i y para n. Así, para calcular la tasa de interés mensual, se divide la tasa anual entre la frecuencia de conversión:

Para determinar n, se multiplica el lapso en años por la frecuencia de conversión:

Factor de monto a interés compuesto:

En dos años, la inversión de $50 000 se transformará en un monto de $71475.14 por la generación de un interés compuesto de $21475.14.

Ejemplo 3:

Se depositan en una caja de ahorros $100 000 a una tasa de interés de 4.8% capitalizable mensualmente.

a) ¿Cuál será el monto acumulado a interés compuesto en un periodo de nueve meses?

b) Suponiendo que la caja de ahorros preste ese mismo dinero con una tasa de interés de 30% anual capitalizable mensualmente, ¿cuál sería el pago que se debe efectuar al cabo

de los mismos 9 meses?

Debemos determinarse la tasa de interés mensual dividiendo la tasa anual entre la frecuencia de conversión:

Puesto que el tiempo de inversión está ya expresado en meses, se tienen todos los elementos necesarios para plantear y resolver el ejemplo:

Así, se sustituyen los valores en la fórmula y se tiene:

Por lo tanto, un depósito de $100 000 rendirá $3 658.10 de interés y acumulará un monto de $103 658.10 al cabo de nueve meses.

b) Préstamo

Para aplicar la fórmula

es necesario determinar la tasa de interés, para lo cual se divide la tasa anual entre la frecuencia de conversión:

Con ello se tienen ya todos los datos necesarios para aplicar dicha fórmula:

Así, se sustituyen los valores en la fórmula y se tiene:

La diferencia que existe entre el monto derivado del préstamo ($124 886.30) y el monto que debe pagar al ahorrador ($103 658.10), esto es, la cantidad de $21228.20, constituye la utilidad del intermediario financiero, en este caso, de la caja de ahorros.

Ejemplo 4:

Se obtiene un préstamo bancario de $1500 000 a un plazo de un año y con interés de 12%

convertible trimestralmente. ¿Cuál es el monto que deberá liquidarse?

Solución:

Se determina primero la tasa de interés por periodo de conversión:

El número de periodos de capitalización n es igual a: 1 año × 4 = 4

Deberá liquidarse al banco la cantidad de $1688 263.22.

Monto compuesto con periodo de interés fraccionario

La fórmula (3.3) se deriva del supuesto de que n es entero. En teoría puede aplicarse también en el caso de que n sea fraccionario, pero para resolverlo sólo puede recurrirse al uso de logaritmos o de la calculadora.

Ejemplo 5:

Se decide liquidar el préstamo del ejemplo anterior en forma anticipada luego del transcurso de 7 meses y medio. ¿Cuál es la cantidad que debe pagarse?

Solución:

7.5/3 meses = 2.5 trimestres

M = 1 500 000 (1 + 0.03)2.5

M = 1 500 000 (1.076696)

M = 1 615 043.86

Una forma práctica de resolverlo es determinar el monto compuesto correspondiente a los periodos completos de conversión y aumentar el interés simple por el periodo fraccionario de conversión a la tasa estipulada.

I compuesto I simple

La diferencia resultante, según la tasa de interés y del tiempo, puede llegar a ser significativa, por lo que siempre que sea posible se recomienda el empleo de la fórmula:

Ejemplo 6

Se contrata un préstamo bancario de habilitación y avío por 150 000 pesos. El plazo de pago es de 3 años. La tasa de interés es de 20% anual convertible semestralmente. ¿Cuál es la cantidad que deberá liquidarse si se decide cancelarlo en forma anticipada a los 15 meses?

Deben liquidarse $190 358.81

Nota: La magnitud de las cifras a veces provoca confusiones y errores por el manejo de los ceros. Por esta razón se recomienda, siempre que sea posible, eliminar ceros y manejar cifras en miles o millones de pesos en los procesos de solución de los problemas. 

Cabe señalar que si bien se utilizan cifras simplificadas en los procesos de solución, el resultado final se expresa en su magnitud original.

Por el método aproximado: